Outline
- The long and winding road (of research)
- Acetone Droplets in a Leidenfrost state
- Soap film singularities
- Suspended rings
- Classical Catenoid
- Calculus of variations formulation
- Experimental verification
- Gravity-mediated platonic solid assemblies
- Surface Evolver simulations
- Displacement-driven prisms and pyramids
- Transient tile angle simulations and modeling
- Effective radii of structures
- Additional geometries
Starting Point: Leidenfrost Effect on a Liquid Substrate

Starting Point: Leidenfrost Effect on a Liquid Substrate
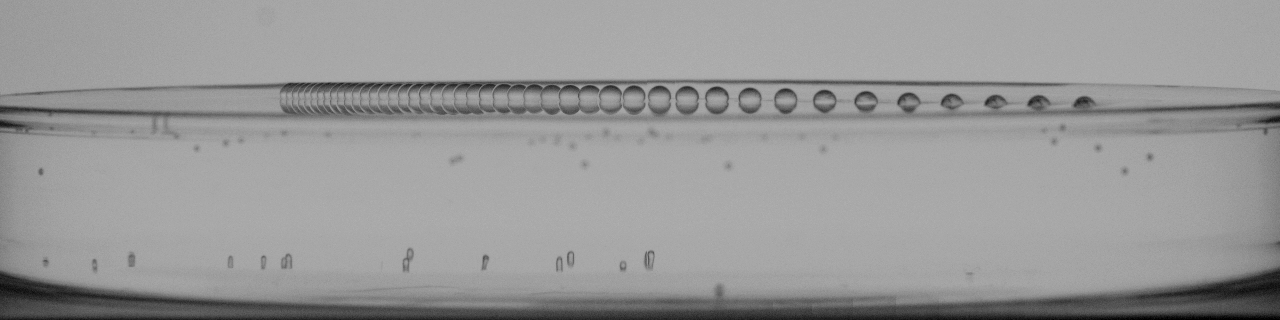

Superposition of 40 frames over an elapsed time of 1 second of an acetone droplet in a Leidenfrost state on water heated to approximately 75 degrees celsius. The white dashed line shows the undisturbed free surface. The tube visible at the far left is the deposition point, the droplets are approximately a 3 and 2.6 mm in diameter.
Analogous Soap Film Experiments

\(90^{\circ}\)

\(85^{\circ}\)

\(80^{\circ}\)

\(55^{\circ}\)
A glass cover slip (dimensions 18x18 mm and 0.15 mm thick) piercing a soap film at different relative angles.
First Gravity Mediated Assembly






Gravity mediated assembly process
- Davies, October 2018
- Davies and Raufaste, June 2021
Catenoid
\[ y = a \cosh \left( \frac{x}{a} \right) \]
- Goldstein et al. September 2021
- Raufaste et al. June 2022
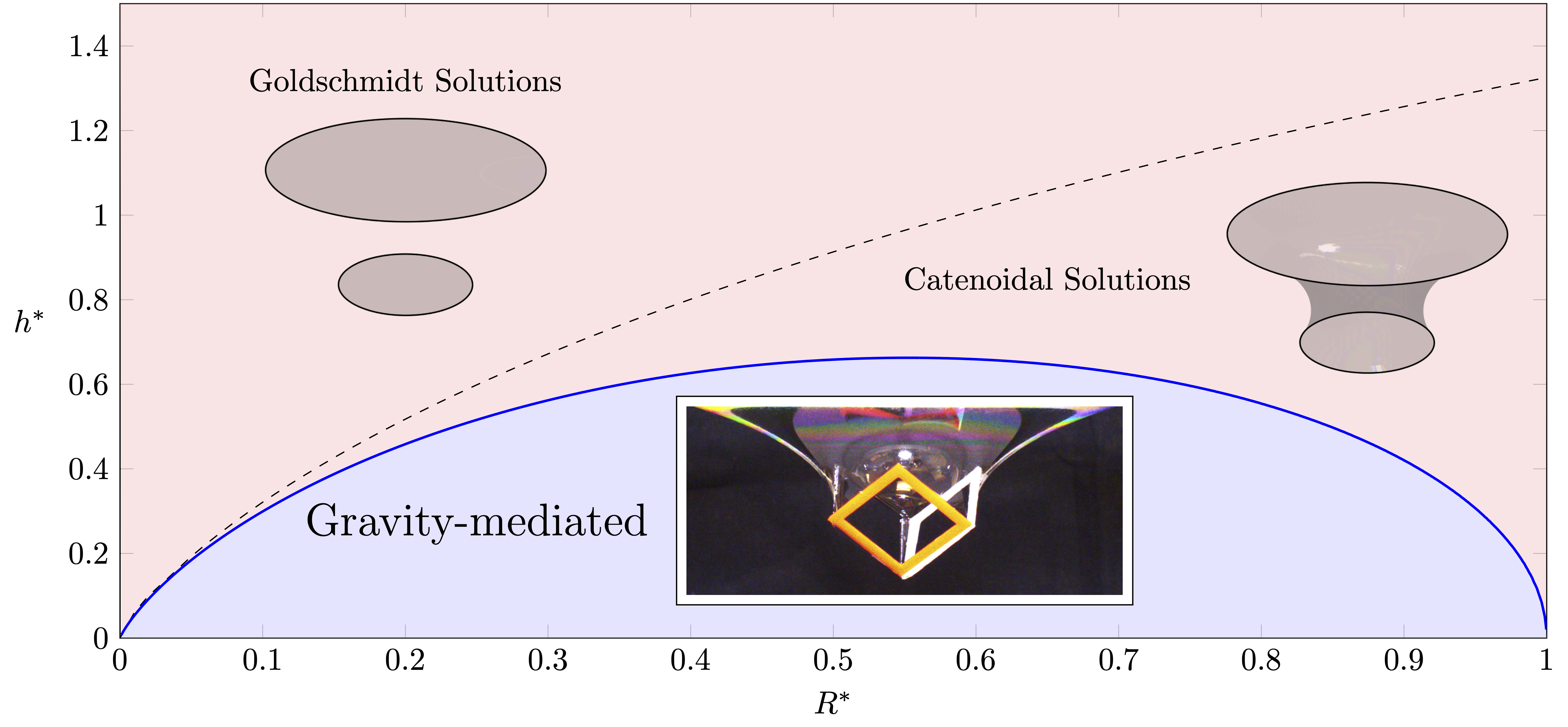
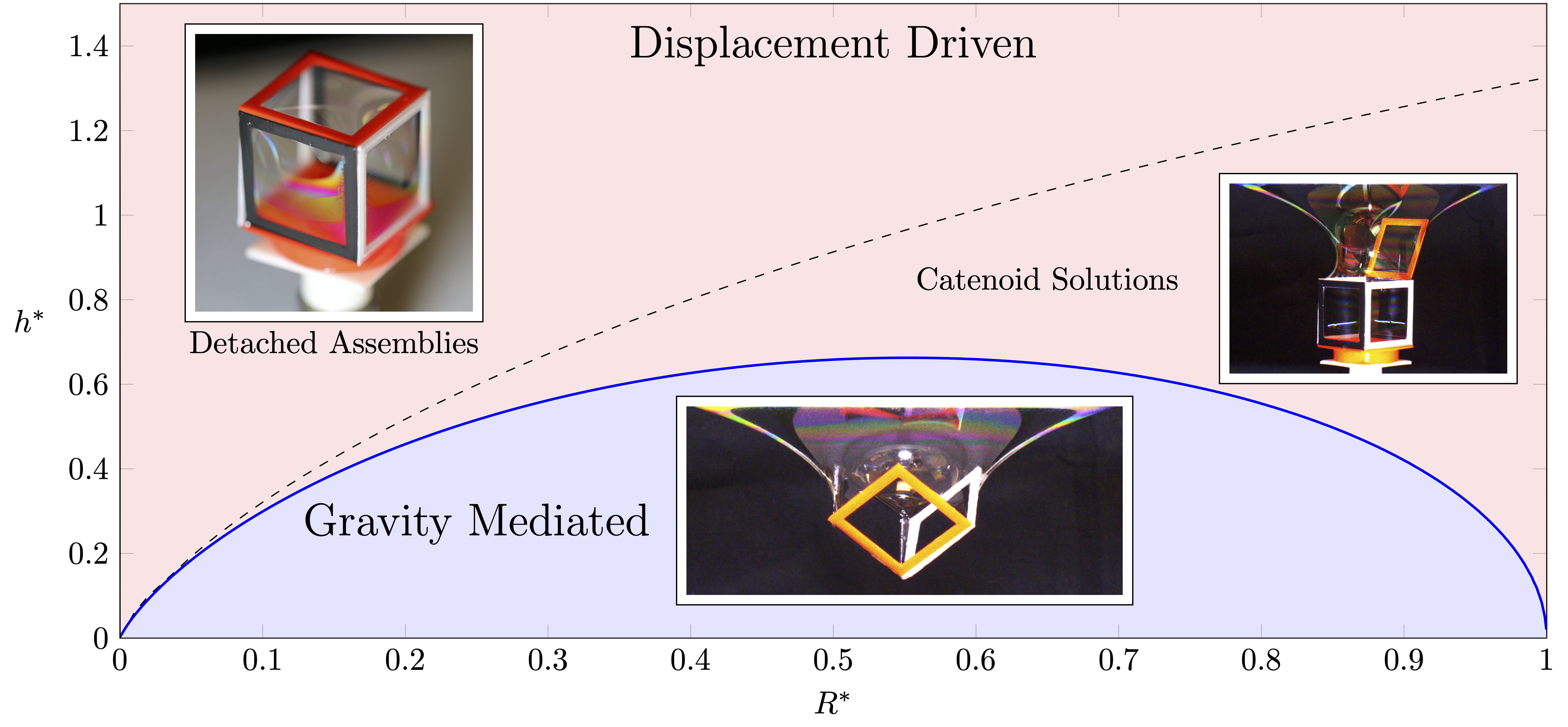
Goldschmidt solutions
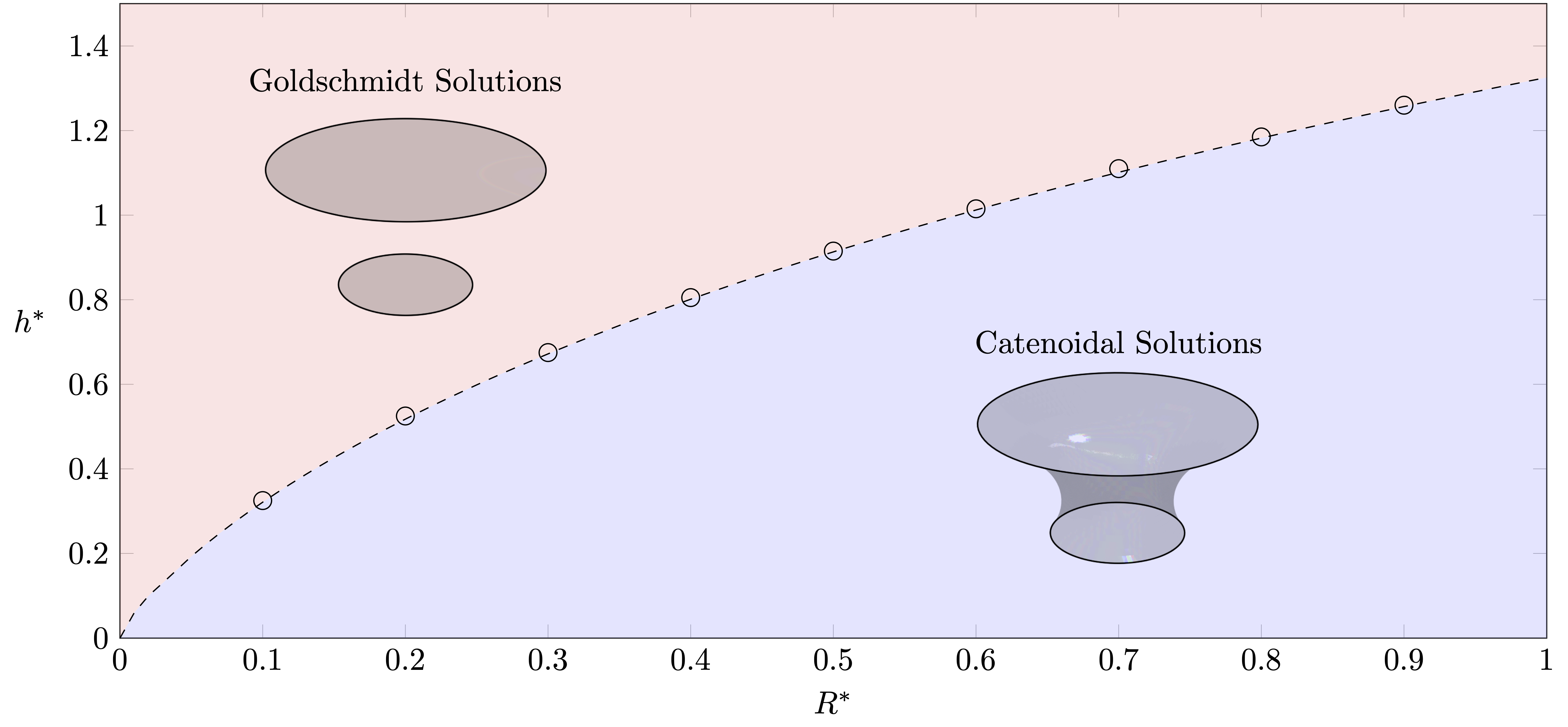
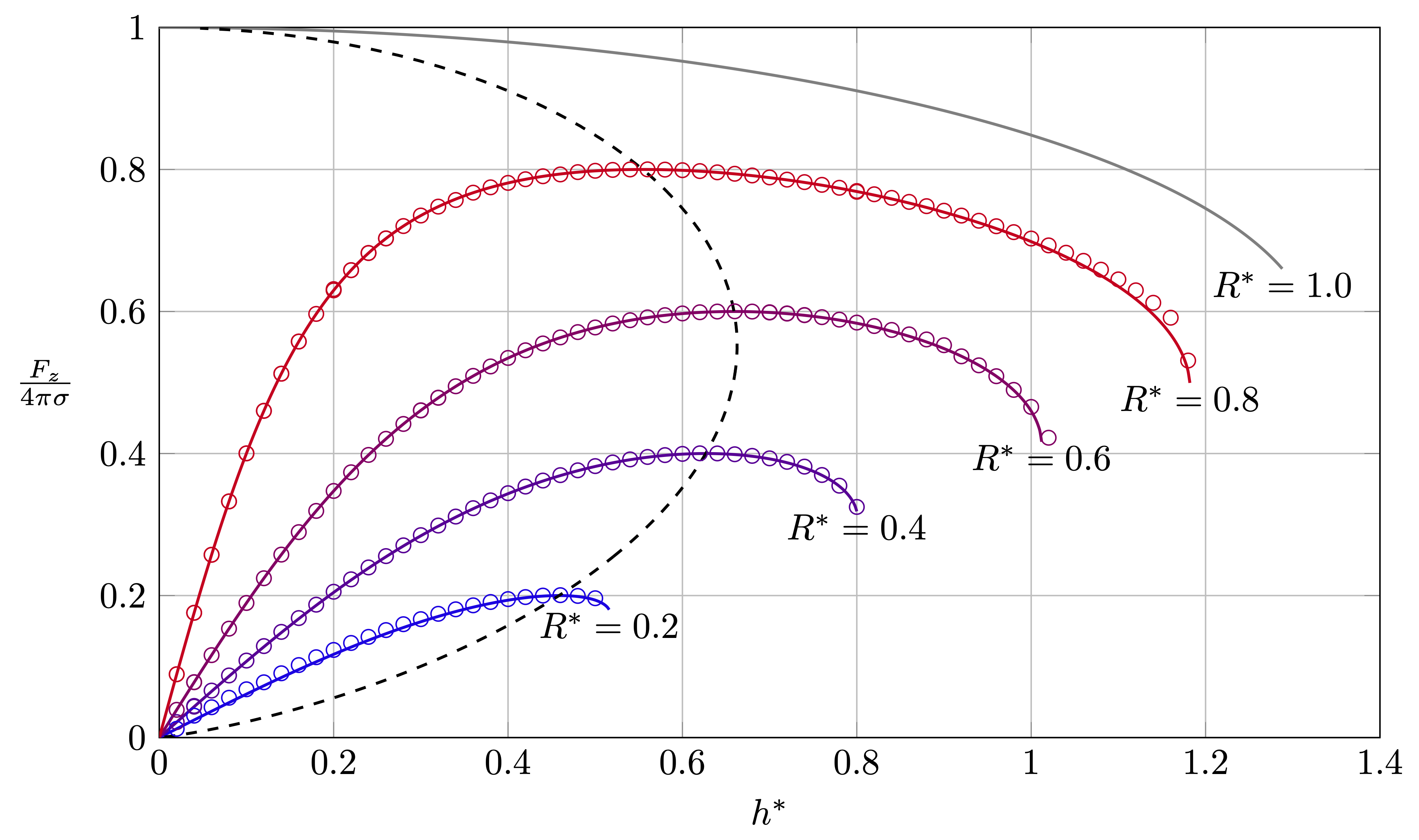
The red region represents combinations of R* and h* yielding Goldschmidt solutions, and in blue are pairs for which a catenoid solution exists. The inset images are simulation results for R*=0.5 and h*=0.91, 0.915 corresponding to catenoidal and Goldschmidt solutions.
Calculus of variations formulation
\[ \begin{align} \mathcal{E} (R,h) &= \int_{0}^{l}2 \sigma( 2\pi R) ds - m g h \nonumber\\ &= \int_{0}^{h}\left[ 4\pi\sigma R\sqrt{1 + (R')^2}\right] \,dz - m g h \nonumber \end{align} \]
Variations \(R+\epsilon\eta\) and \(h+\epsilon k\) are considered for some parameter \(\epsilon\ll1\) with two constraints on the variations.
\[ \eta (0) = 0 \qquad \qquad \eta (h) = -k R'(h) \]
First Variation Condition and BVP
The first-variation condition for the energy functional can be written as \[ \begin{equation} \scriptsize{ 0=\bbox[5px, border: 2px solid red]{\int_{0}^{h} 4\pi\sigma \eta \left[ \sqrt{1 + (R')^2} - \frac{\mathrm{d}}{\mathrm{d} z} \left(\frac{R R'}{\sqrt{1 + (R')^2}}\right)\right] \,dz} + \bbox[5px, border: 2px solid blue]{ k\left[ 4\pi\sigma R_i\sqrt{1 + (R'(h))^2} - mg - \frac{4 \pi \sigma R_i (R'(h))^2}{\sqrt{1 + (R'(h))^2}} \right]} } \end{equation} \]
with the following corresponding terms of the boundary value problem \[ \begin{equation} \bbox[5px, border: 2px solid red]{0 = 1 + R'(z)^2 - R(z)R''(z)} \end{equation} \]
\[ \begin{equation} \bbox[5px, border: 2px solid blue]{(R'(h))^2 = \frac{1}{B^{2}} - 1} \end{equation} \]
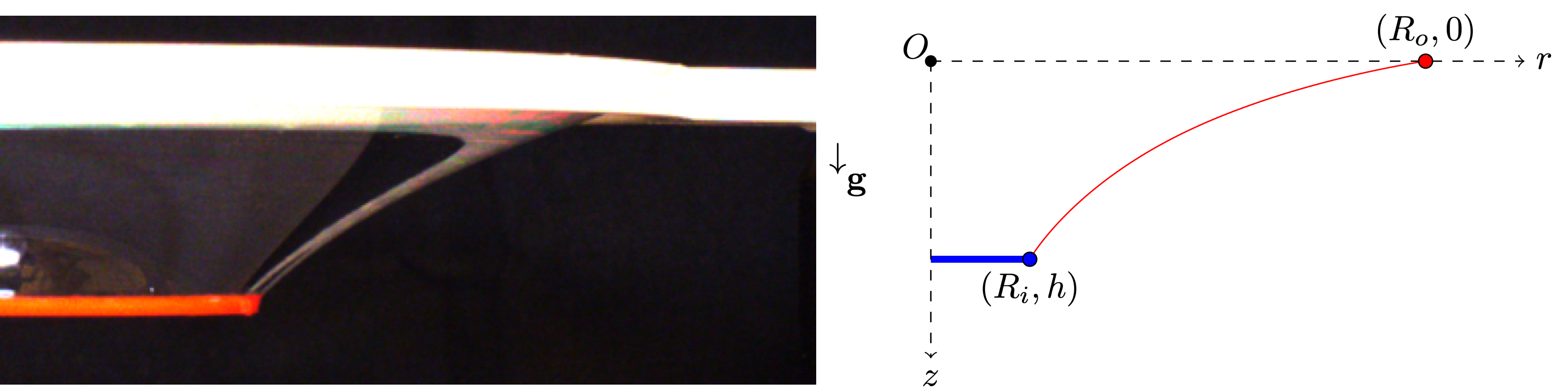
Where the Bond number of the system is given by \(B=mg/ 4\pi\sigma R_i\) and \(R(0)=R_i\) is the boundary condition at the supporting ring.
Closed form solution
\[ \begin{equation} R(z) = \frac{mg}{4\pi\sigma} \cosh\left( \frac{4\pi\sigma z}{mg}+\cosh^{-1}\left(\frac{4\pi\sigma R_o}{mg}\right) \right) \end{equation} \]
Evaluating the above equation at \((R_i,h)\) and solving for \(h\) yields \[ \begin{equation} h = \frac{mg}{4\pi\sigma}\left[ \cosh^{-1}\left(\frac{4\pi\sigma R_i}{mg}\right)-\cosh^{-1}\left(\frac{4\pi\sigma R_o}{mg}\right)\right] \end{equation} \]
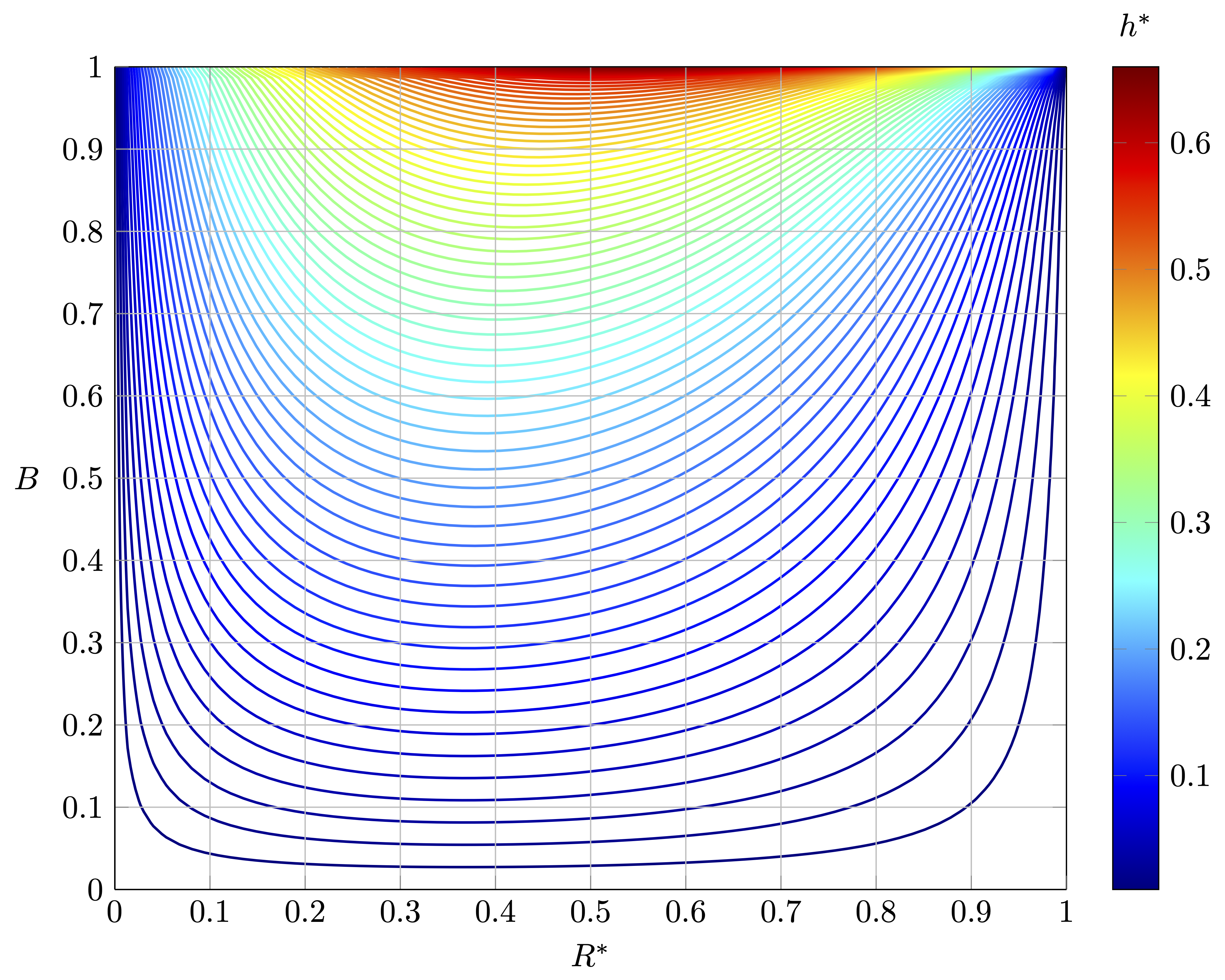
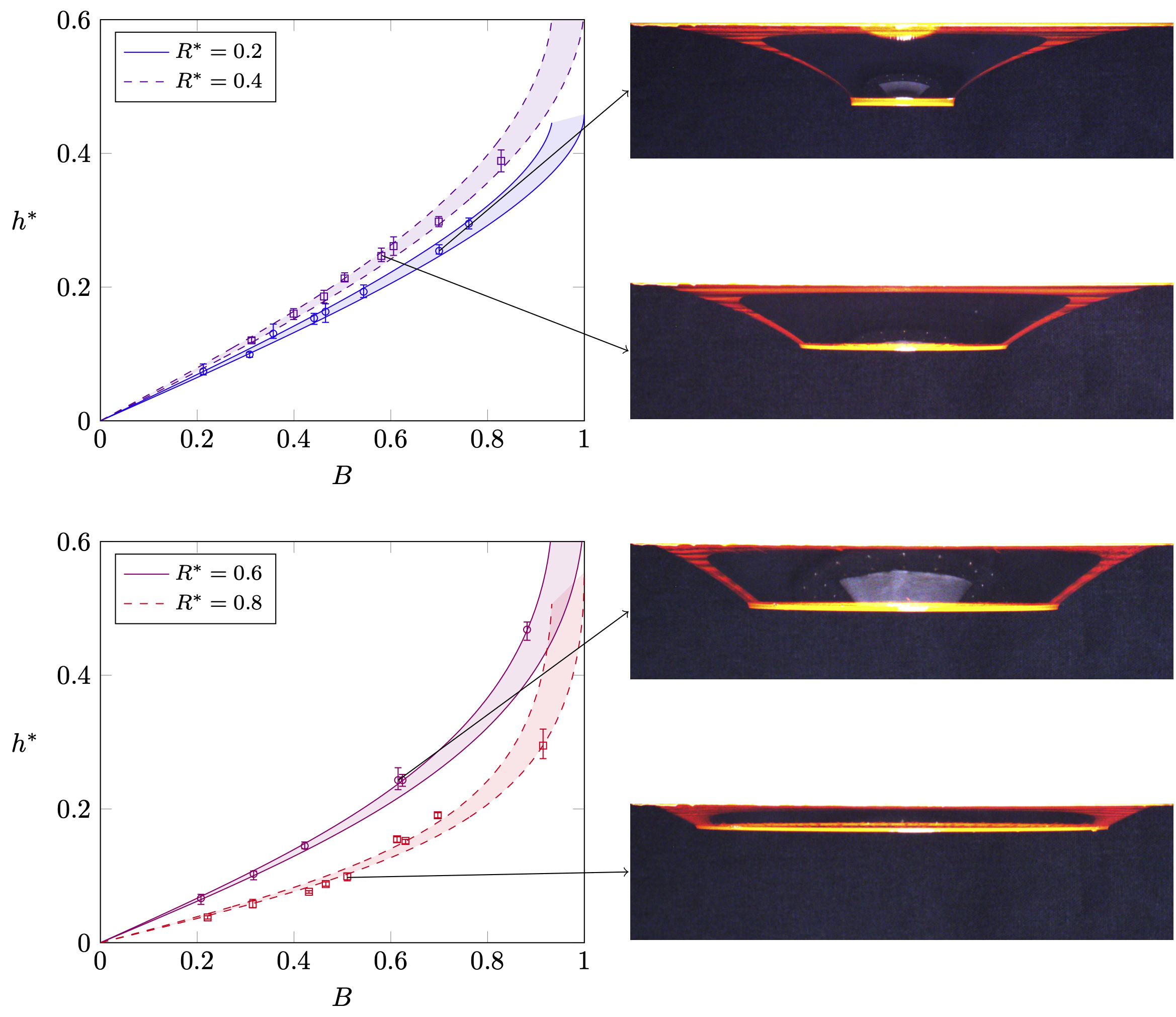
Letting \( R^*=R_i /R_o \) and \( h^*=h /R_o \) in addition to \(B=mg/ 4\pi\sigma R_i\) \[ \begin{equation} \bbox[5px, border: 2px solid red] { h^* = B R^* \left(\cosh^{-1}\frac{1}{B}-\cosh^{-1}\frac{1}{B R^*}\right) } \end{equation} \]
Contour Plot
\[ \scriptsize{ \begin{equation} h^* = B R^* \left(\cosh^{-1}\frac{1}{B}-\cosh^{-1}\frac{1}{B R^*}\right) \end{equation} } \]
Experimental results of suspended rings
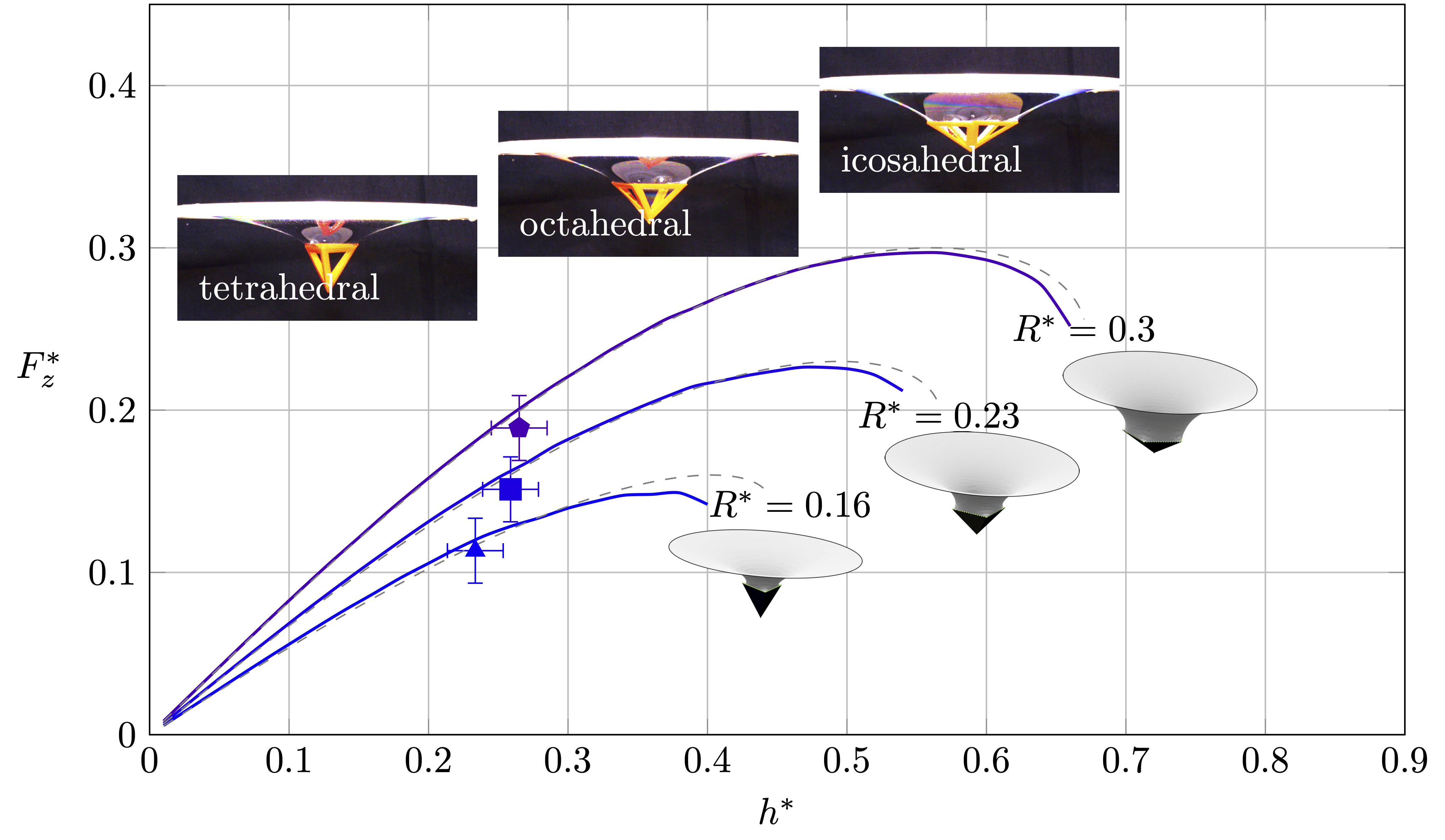
Platonic solid geometries

Platonic solid geometries

Surface Evolver simulations
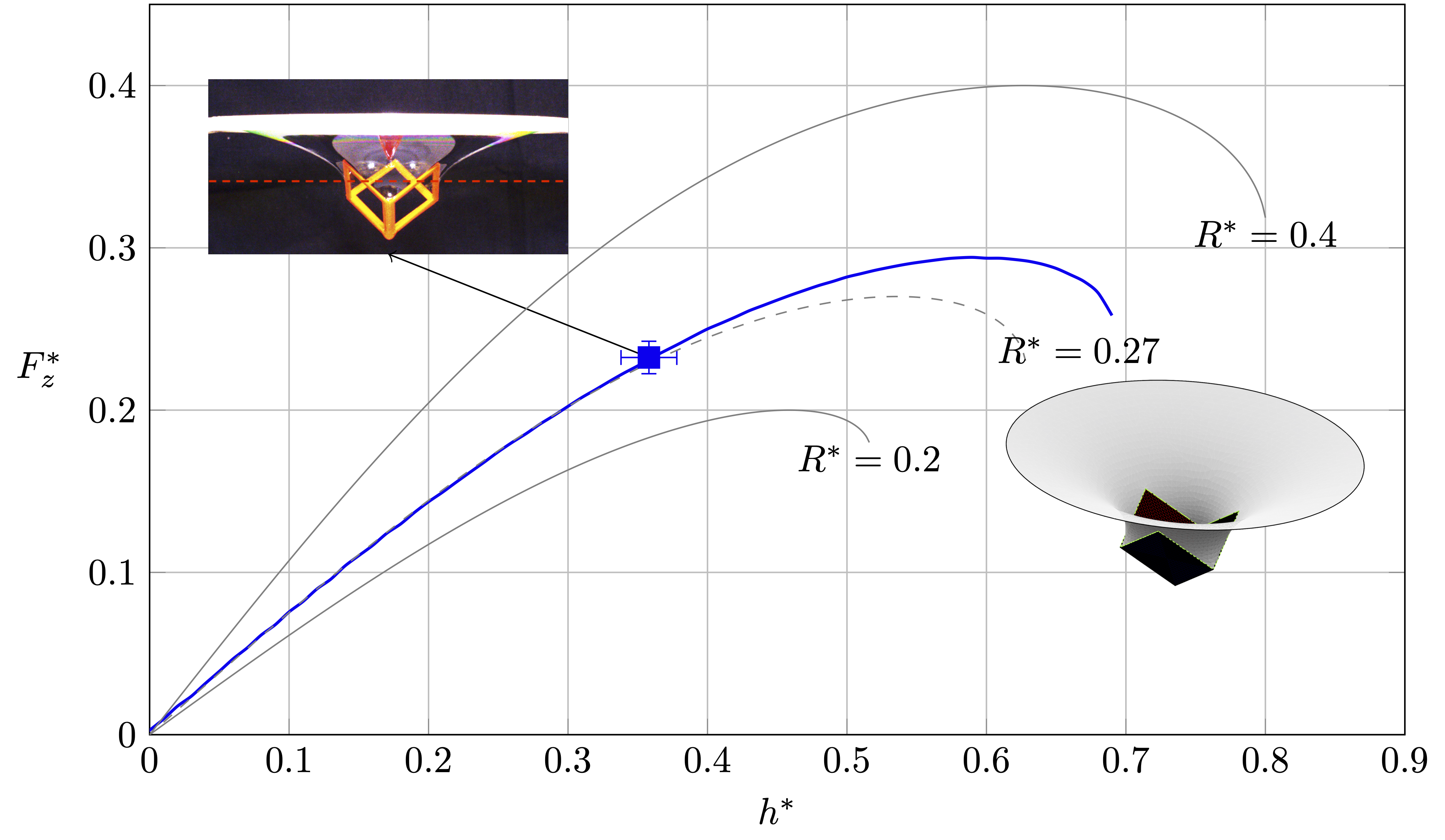
Gravity-mediated assemblies phase space
Displacement-driven assembly setup
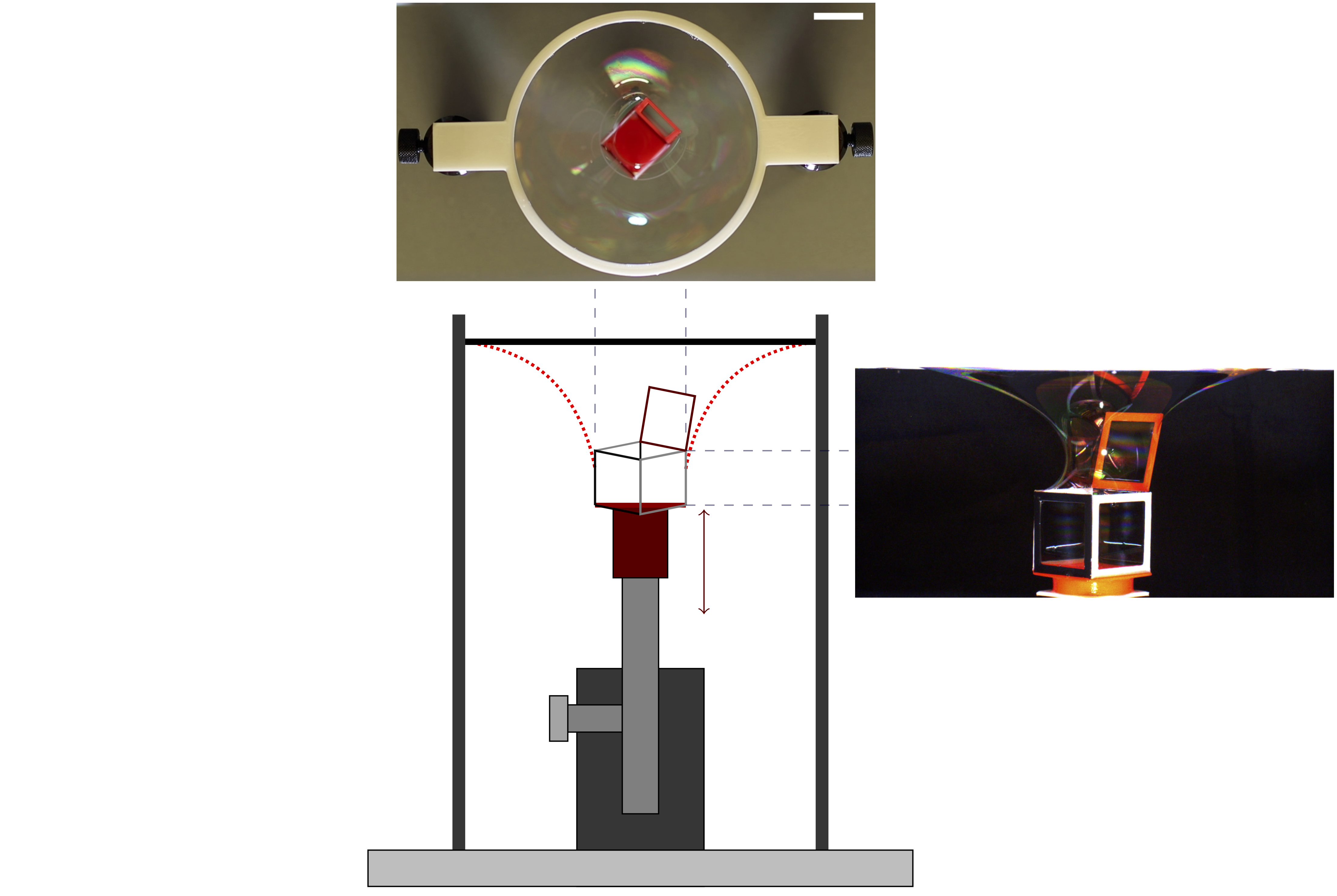
Rectangular prisms

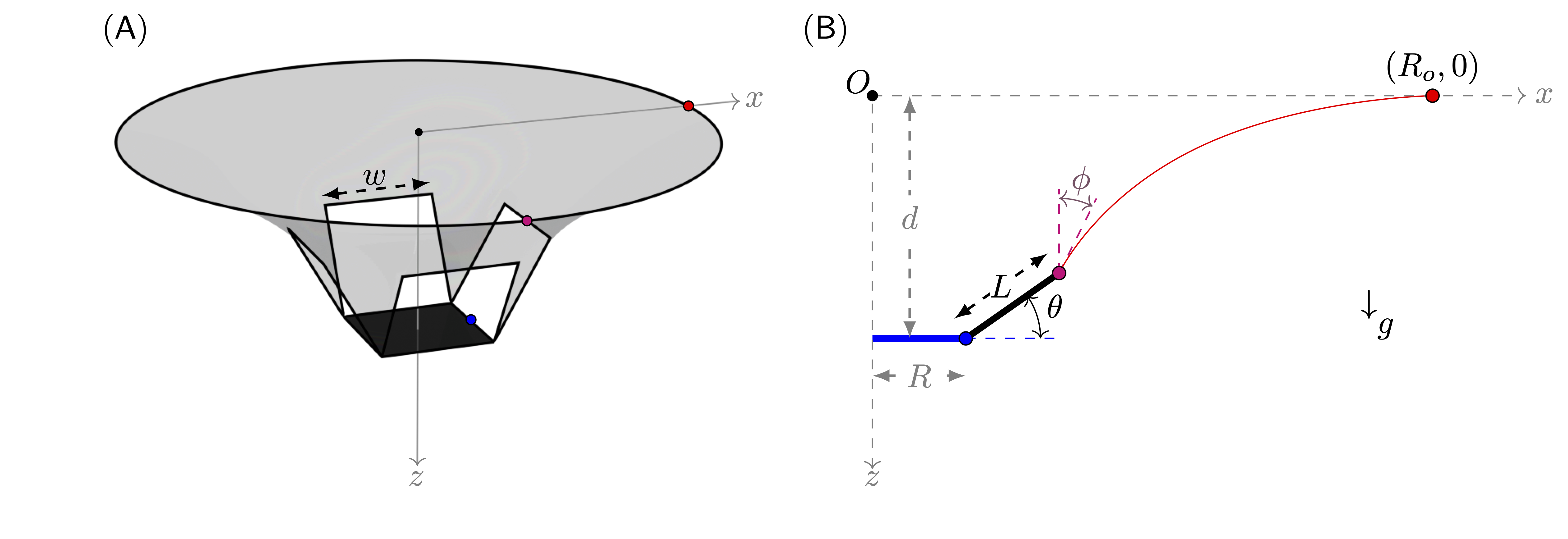
\[ \begin{equation} \mathcal{T}_g=\frac{Lmg\cos\theta}{2}, \qquad \mathcal{T}_\sigma=2Lw\sigma\cos(\theta+\phi), \qquad B_t = \frac{mg}{4w\sigma} \end{equation} \]
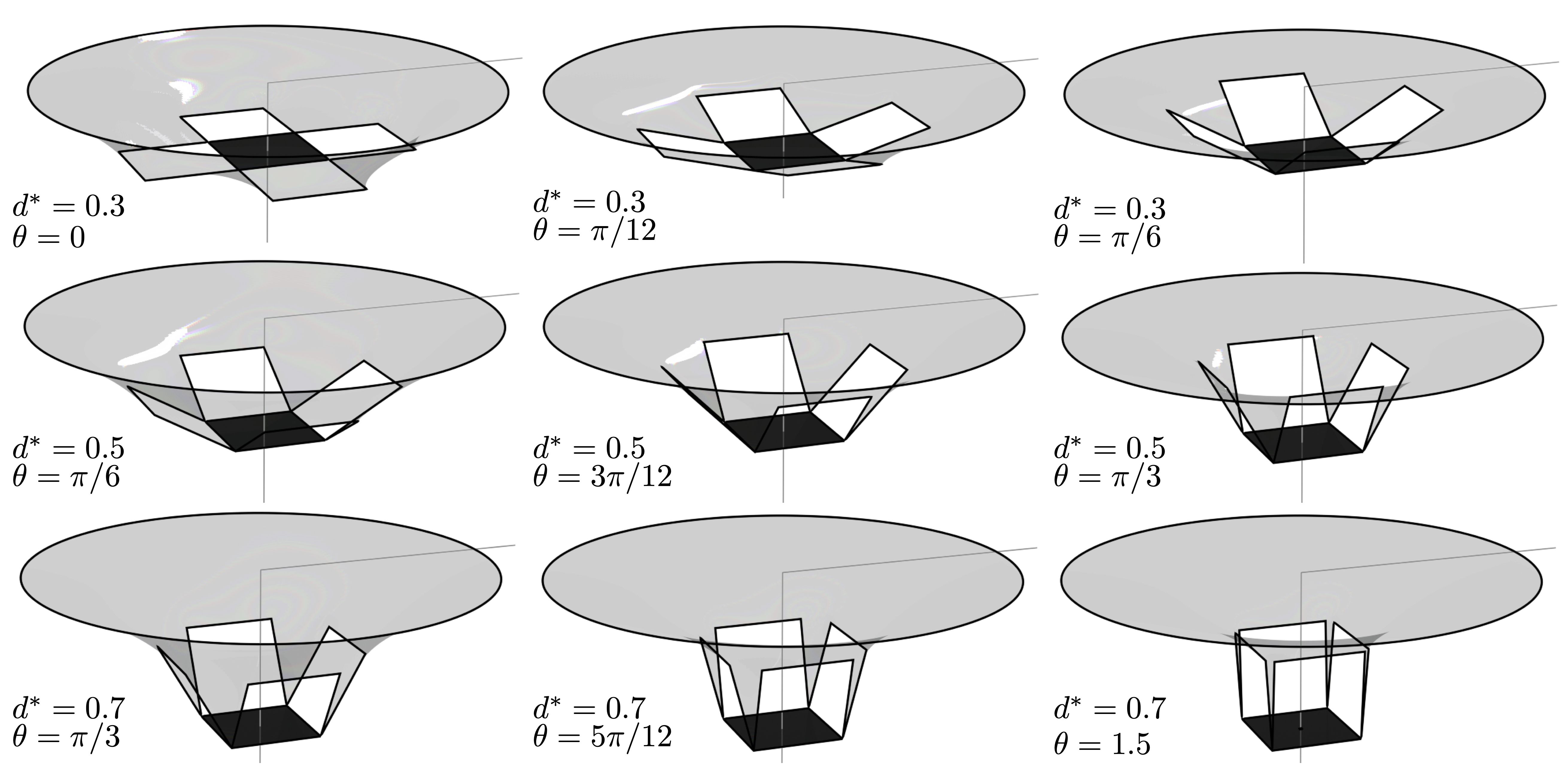
Surface Evolver simulations of transient tile angles
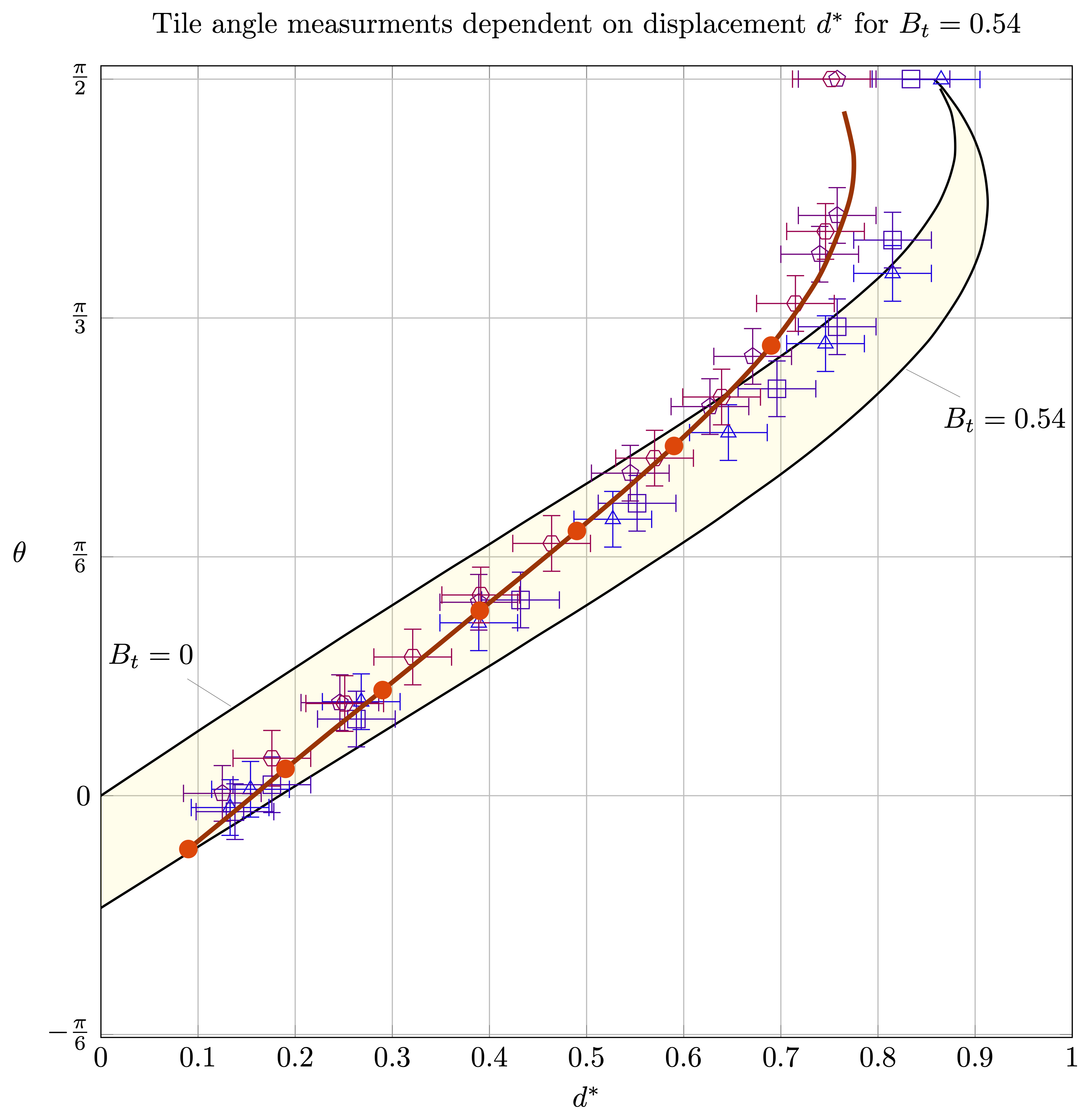
Surface Evolver simulations compared to experimental results
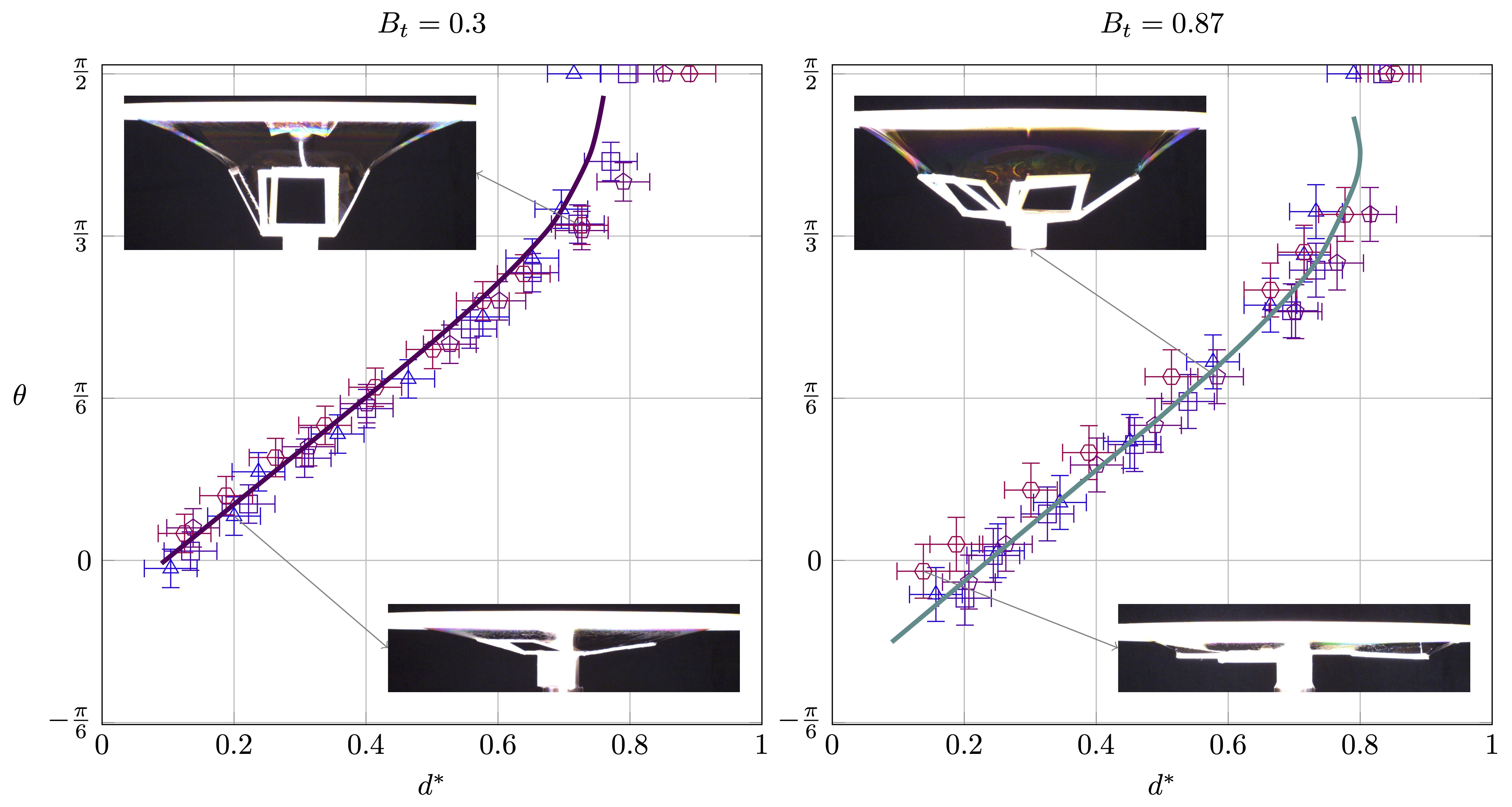
Addition of mathematical model

Effective radius for prismatic pinch-off

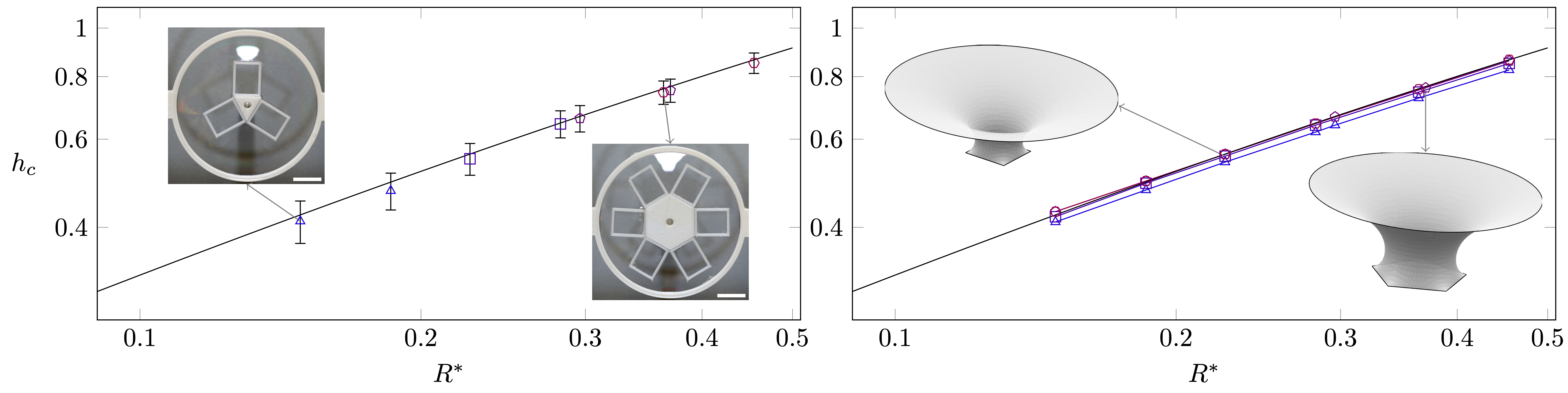
Effective radius for pyramidal pinch-off

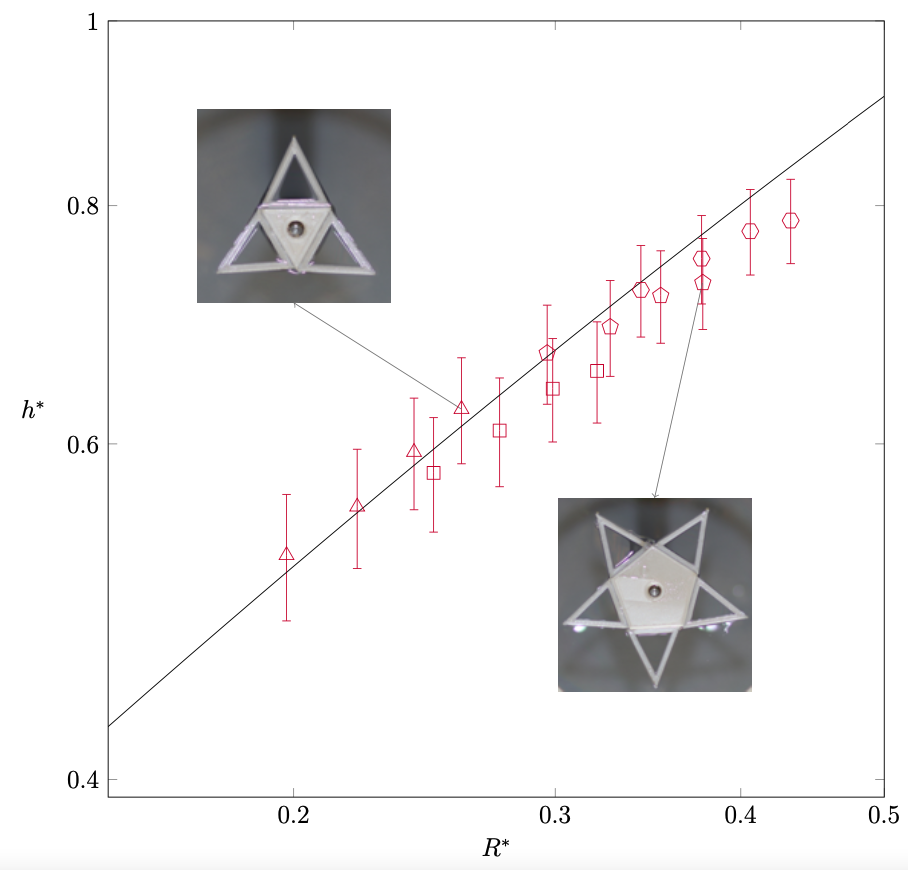
Soap film mediated assembly
Additional geometries
Thank you!

Thank you!



ありがとうございます
Surface Evolver simulations
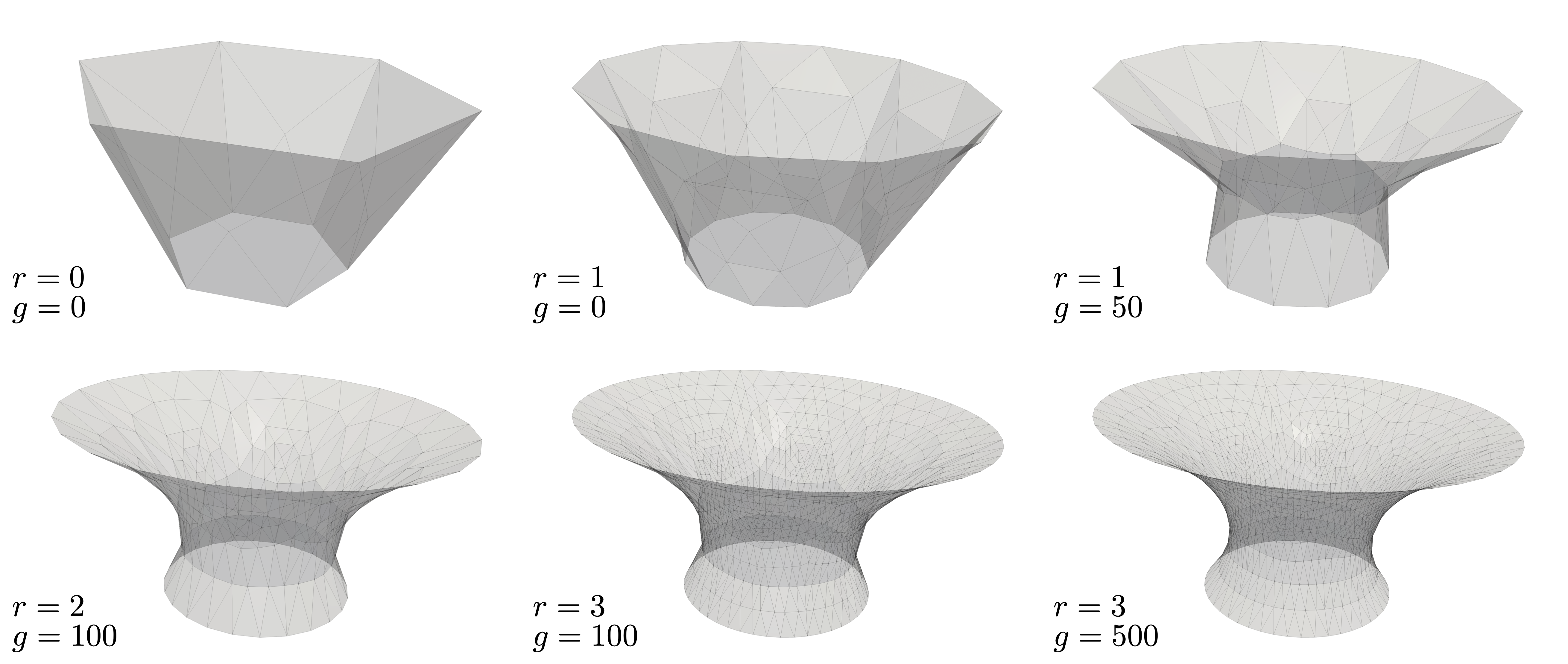
Examples of refinement (r) and iteration (g) operations within a Surface Evolver simulation of a catenoid where R*=0.5 and h*=0.9.
Calculus of variations formulation continued
Let \(\mathcal{F}\) be defined by \(\mathcal{F} ( \epsilon) =\mathcal{E}(R+\epsilon\eta,h+\epsilon k)\) \[ \begin{align} \mathcal{F} &= \int_{0}^{h + \epsilon k}\left[ 4\pi\sigma (R+\epsilon \eta)\sqrt{1 + (R'+\epsilon \eta')^2} \right] \,dz - mg(h+\epsilon k) \\ \end{align} \]
Granted that R and h correspond to a minimum of the potential energy functional, the Gateaux derivative of \(\mathcal{F} \) must vanish at \(\epsilon=0\): \[ \begin{equation} \frac{\mathrm{d}\mathcal{F}(\epsilon)}{\mathrm{d}\epsilon}\bigg|_{\epsilon=0}=0 \end{equation} \]
Two constraints on the variations arise from the boundary conditions \[ \eta (0) = 0 \qquad \qquad \eta (h) = -k R'(h) \]
Verification of Surface Evolver simulations
Model of transient tile angle
The equilibrium condition \(\mathcal{T}_g=\mathcal{T}_\sigma \) can be expressed as \[ \begin{equation} B_t = \frac{mg}{4 w \sigma}=\frac{\cos(\phi+\theta)}{\cos\theta} \end{equation} \]
Under the assumption that a cross-section of the soap film can be represented as a catenary curve \[ \scriptsize{ \begin{equation} d^* = (R^*+L^*\cos\theta) g(B_t,\theta)\Big[ \cosh^{-1} \left(\frac{1}{g(B_t,\theta)}\right) - \cosh^{-1} \left( \frac{1}{ (R^*+L^*\cos\theta) g(B_t,\theta) }\right) \Big] + L^*\sin\theta \end{equation} } \]
where the function \( g(B_t,\theta) \) is given by \[ \begin{equation} g(B_t,\theta)=\cos[\cos^{-1} ( B_t\cos\theta)-\theta], \qquad 0\le B_t\le1.1547, \qquad -\frac{\pi}{6}\le\theta\le\frac{\pi}{2} \end{equation} \]
Transient tile angle experiments
Competition between torques due to gravity and surface tension
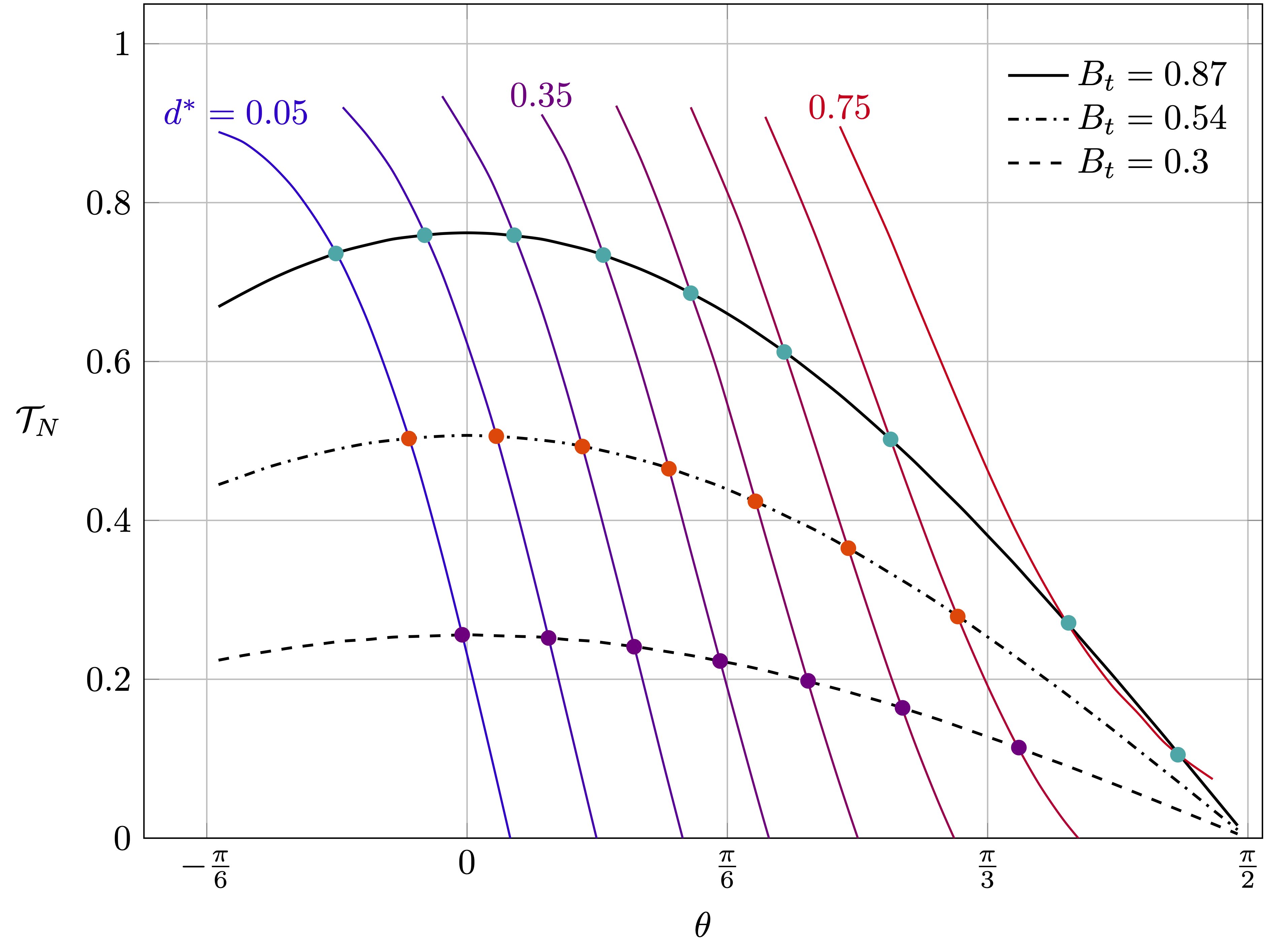
Surface Evolver simulations compared to experimental results
Displacement driven octahedral assembly
Displacement driven pentagonal prism assembly
Pentagonal prism reversibility
Displacement driven pentagonal pyramid assembly
Pentagonal pyramid reversibility
